旅行笔记：费马小定理（素性测试）（1）

0.前言

是这样的，前一个月回老家了，没带电脑，只带了游戏机和几本乱七八糟的书。

在老家大部分时间都在打MHR，但是书姑且也翻了翻，就随便记录了一些东西。

“旅行笔记”系列是对出门在外期间的纸质笔记的整理，不仅仅是这次回老家，也许以后的也会放到blog上。

因为是随便记的，所以什么都会有，也比较乱。

1.费马小定理

如果$p$是一个素数，那么对于任意的$1\le a<p$，有

$a^{p-1}\equiv1(mod\ p)$

---

比如，对于$a=3,p=7$而言：

$mod\ p$之后可能得到的非零结果集合为$(1,2,\dots,6)$

该集合与以下集合是相等的：

$(3\cdot 1\ mod\ 7$

$3\cdot 2\ mod\ 7$

$3\cdot 3\ mod\ 7$

$\dots$

$3\cdot 6\ mod\ 7)$

事实上，第二个集合的元素就是第一个集合的元素的重排：

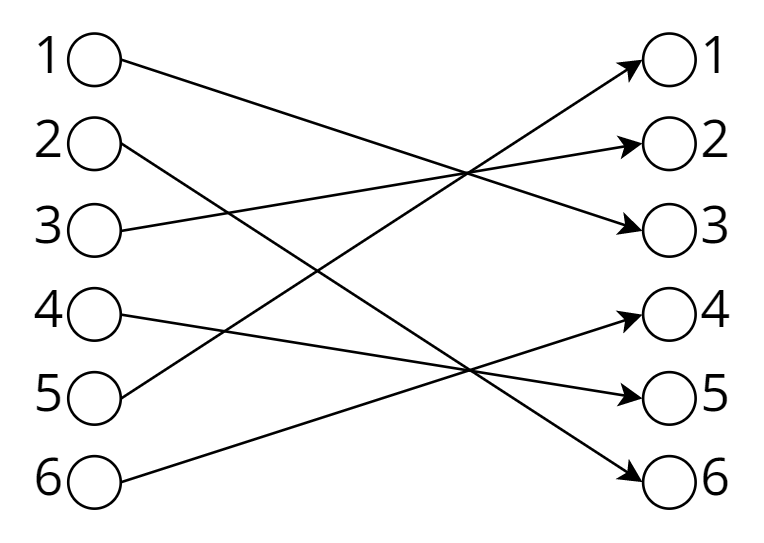
然后对于两个集合，有：

$1\cdot2\cdot3\cdot4\cdot5\cdot6 \equiv 3^6\cdot 1\cdot2\cdot3\cdot4\cdot5\cdot6\ (mod\ 7)$

$3^6 \equiv1\ (mod\ 7)$

2.Carmichael数

所有素数都能通过素性测试，但并不是通过素性测试的都是素数。

Carmichael数就是能够通过费马素性测试的合数。

3.一个引理

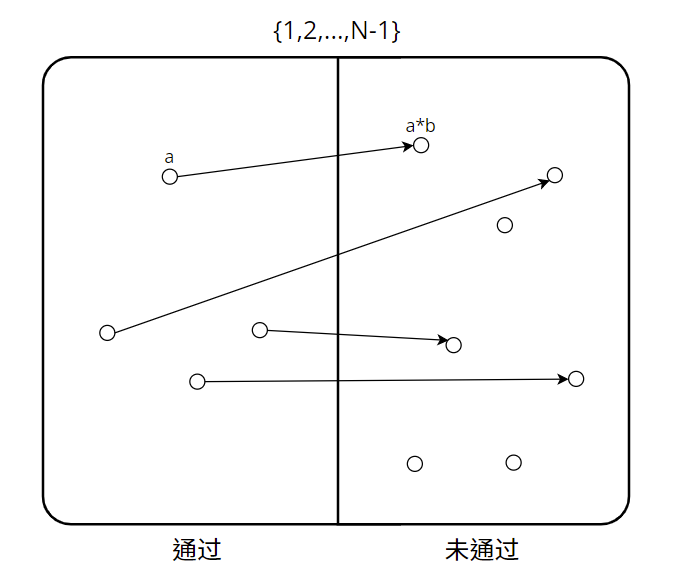
引理：如果对于某些与$N$互素的$a$，有$a^{N-1} \not\equiv 1\ mod\ N$，那么对于$a<N$的至少一半的可能取值，$N$将无法通过费马测试。

这是因为对于每一个能够通过费马测试的数$b$，都有一个数$a\cdot b$，无法通过费马测试。

如下图：（左侧的应该是$b$，做图的时候打错了）